
SL Paper 2
A pipe is open at both ends. A first-harmonic standing wave is set up in the pipe. The diagram shows the variation of displacement of air molecules in the pipe with distance along the pipe at time t = 0. The frequency of the first harmonic is f.
A transmitter of electromagnetic waves is next to a long straight vertical wall that acts as a plane mirror to the waves. An observer on a boat detects the waves both directly and as an image from the other side of the wall. The diagram shows one ray from the transmitter reflected at the wall and the position of the image.
An air molecule is situated at point X in the pipe at t = 0. Describe the motion of this air molecule during one complete cycle of the standing wave beginning from t = 0.
The speed of sound c for longitudinal waves in air is given by
where ρ is the density of the air and K is a constant.
A student measures f to be 120 Hz when the length of the pipe is 1.4 m. The density of the air in the pipe is 1.3 kg m–3. Determine, in kg m–1 s–2, the value of K for air.
Demonstrate, using a second ray, that the image appears to come from the position indicated.
Outline why the observer detects a series of increases and decreases in the intensity of the received signal as the boat moves along the line XY.
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
The beam is incident normally on a double slit. The distance between the slits is 0.300 mm. A screen is at a distance D from the slits. The diffraction angle θ is labelled.
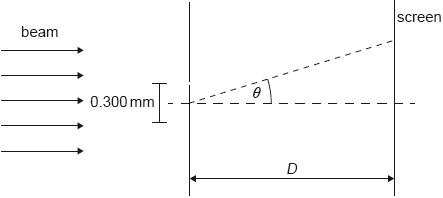
The air between the slits and the screen is replaced with water. The refractive index of water is 1.33.
A series of dark and bright fringes appears on the screen. Explain how a dark fringe is formed.
The wavelength of the beam as observed on Earth is 633.0 nm. The separation between a dark and a bright fringe on the screen is 4.50 mm. Calculate D.
Calculate the wavelength of the light in water.
State two ways in which the intensity pattern on the screen changes.
The solid line in the graph shows the variation with distance of the displacement of a travelling wave at t = 0. The dotted line shows the wave 0.20 ms later. The period of the wave is longer than 0.20 ms.
One end of a string is attached to an oscillator and the other is fixed to a wall. When the frequency of the oscillator is 360 Hz the standing wave shown is formed on the string.
Point X (not shown) is a point on the string at a distance of 10 cm from the oscillator.
Calculate, in m s–1, the speed for this wave.
Calculate, in Hz, the frequency for this wave.
The graph also shows the displacement of two particles, P and Q, in the medium at t = 0. State and explain which particle has the larger magnitude of acceleration at t = 0.
State the number of all other points on the string that have the same amplitude and phase as X.
The frequency of the oscillator is reduced to 120 Hz. On the diagram, draw the standing wave that will be formed on the string.
A vertical tube, open at both ends, is completely immersed in a container of water. A loudspeaker above the container connected to a signal generator emits sound. As the tube is raised the loudness of the sound heard reaches a maximum because a standing wave has formed in the tube.
Describe two ways in which standing waves differ from travelling waves.
Outline how a standing wave forms in the tube.
The tube is raised until the loudness of the sound reaches a maximum for a second time.
Draw, on the following diagram, the position of the nodes in the tube when the second maximum is heard.
Between the first and second positions of maximum loudness, the tube is raised through 0.37 m. The speed of sound in the air in the tube is 320 m s−1. Determine the frequency of the sound emitted by the loudspeaker.
A loudspeaker emits sound waves of frequency towards a metal plate that reflects the waves. A small microphone is moved along the line from the metal plate to the loudspeaker. The intensity of sound detected at the microphone as it moves varies regularly between maximum and minimum values.
The speed of sound in air is 340 m s−1.
Explain the variation in intensity.
Adjacent minima are separated by a distance of 0.12 m. Calculate .
The metal plate is replaced by a wooden plate that reflects a lower intensity sound wave than the metal plate.
State and explain the differences between the sound intensities detected by the same microphone with the metal plate and the wooden plate.
The diagram shows the direction of a sound wave travelling in a metal sheet.
The frequency of the sound wave in the metal is 250 Hz.
Particle P in the metal sheet performs simple harmonic oscillations. When the displacement of P is 3.2 μm the magnitude of its acceleration is 7.9 m s-2. Calculate the magnitude of the acceleration of P when its displacement is 2.3 μm.
The wave is incident at point Q on the metal–air boundary. The wave makes an angle of 54° with the normal at Q. The speed of sound in the metal is 6010 m s–1 and the speed of sound in air is 340 m s–1. Calculate the angle between the normal at Q and the direction of the wave in air.
State the frequency of the wave in air.
Determine the wavelength of the wave in air.
The sound wave in air in (c) enters a pipe that is open at both ends. The diagram shows the displacement, at a particular time T, of the standing wave that is set up in the pipe.
On the diagram, at time T, label with the letter C a point in the pipe that is at the centre of a compression.
A student investigates how light can be used to measure the speed of a toy train.
Light from a laser is incident on a double slit. The light from the slits is detected by a light sensor attached to the train.
The graph shows the variation with time of the output voltage from the light sensor as the train moves parallel to the slits. The output voltage is proportional to the intensity of light incident on the sensor.
Explain, with reference to the light passing through the slits, why a series of voltage peaks occurs.
The slits are separated by 1.5 mm and the laser light has a wavelength of 6.3 x 10–7 m. The slits are 5.0 m from the train track. Calculate the separation between two adjacent positions of the train when the output voltage is at a maximum.
Estimate the speed of the train.
In another experiment the student replaces the light sensor with a sound sensor. The train travels away from a loudspeaker that is emitting sound waves of constant amplitude and frequency towards a reflecting barrier.
The sound sensor gives a graph of the variation of output voltage with time along the track that is similar in shape to the graph shown in the resource. Explain how this effect arises.
A beam of microwaves is incident normally on a pair of identical narrow slits S1 and S2.
When a microwave receiver is initially placed at W which is equidistant from the slits, a maximum in intensity is observed. The receiver is then moved towards Z along a line parallel to the slits. Intensity maxima are observed at X and Y with one minimum between them. W, X and Y are consecutive maxima.
Explain why intensity maxima are observed at X and Y.
The distance from S1 to Y is 1.243 m and the distance from S2 to Y is 1.181 m.
Determine the frequency of the microwaves.
Outline one reason why the maxima observed at W, X and Y will have different intensities from each other.
A large cube is formed from ice. A light ray is incident from a vacuum at an angle of 46˚ to the normal on one surface of the cube. The light ray is parallel to the plane of one of the sides of the cube. The angle of refraction inside the cube is 33˚.
Each side of the ice cube is 0.75 m in length. The initial temperature of the ice cube is –20 °C.
Calculate the speed of light inside the ice cube.
Show that no light emerges from side AB.
Sketch, on the diagram, the subsequent path of the light ray.
Determine the energy required to melt all of the ice from –20 °C to water at a temperature of 0 °C.
Specific latent heat of fusion of ice = 330 kJ kg–1
Specific heat capacity of ice = 2.1 kJ kg–1 k–1
Density of ice = 920 kg m–3
Outline the difference between the molecular structure of a solid and a liquid.
On a guitar, the strings played vibrate between two fixed points. The frequency of vibration is modified by changing the string length using a finger. The different strings have different wave speeds. When a string is plucked, a standing wave forms between the bridge and the finger.
The string is displaced 0.4 cm at point P to sound the guitar. Point P on the string vibrates with simple harmonic motion (shm) in its first harmonic with a frequency of 195 Hz. The sounding length of the string is 62 cm.
Outline how a standing wave is produced on the string.
Show that the speed of the wave on the string is about 240 m s−1.
Sketch a graph to show how the acceleration of point P varies with its displacement from the rest position.
A loudspeaker emits sound towards the open end of a pipe. The other end is closed. A standing wave is formed in the pipe. The diagram represents the displacement of molecules of air in the pipe at an instant of time.
X and Y represent the equilibrium positions of two air molecules in the pipe. The arrow represents the velocity of the molecule at Y.
The loudspeaker in (a) now emits sound towards an air–water boundary. A, B and C are parallel wavefronts emitted by the loudspeaker. The parts of wavefronts A and B in water are not shown. Wavefront C has not yet entered the water.
Outline how the standing wave is formed.
Draw an arrow on the diagram to represent the direction of motion of the molecule at X.
Label a position N that is a node of the standing wave.
The speed of sound is 340 m s–1 and the length of the pipe is 0.30 m. Calculate, in Hz, the frequency of the sound.
The speed of sound in air is 340 m s–1 and in water it is 1500 m s–1.
The wavefronts make an angle θ with the surface of the water. Determine the maximum angle, θmax, at which the sound can enter water. Give your answer to the correct number of significant figures.
Draw lines on the diagram to complete wavefronts A and B in water for θ < θmax.
Two loudspeakers, A and B, are driven in phase and with the same amplitude at a frequency of . Point P is located from A and from B. The speed of sound is .
Deduce that a minimum intensity of sound is heard at P.
A microphone moves along the line from P to Q. PQ is normal to the line midway between the loudspeakers.
The intensity of sound is detected by the microphone. Predict the variation of detected intensity as the microphone moves from P to Q.
When both loudspeakers are operating, the intensity of sound recorded at Q is . Loudspeaker B is now disconnected. Loudspeaker A continues to emit sound with unchanged amplitude and frequency. The intensity of sound recorded at Q changes to .
Estimate .
Two loudspeakers A and B are initially equidistant from a microphone M. The frequency and intensity emitted by A and B are the same. A and B emit sound in phase. A is fixed in position.
B is moved slowly away from M along the line MP. The graph shows the variation with distance travelled by B of the received intensity at M.
Explain why the received intensity varies between maximum and minimum values.
State and explain the wavelength of the sound measured at M.
B is placed at the first minimum. The frequency is then changed until the received intensity is again at a maximum.
Show that the lowest frequency at which the intensity maximum can occur is about 3 kHz.
Speed of sound = 340 m s−1
Outline what is meant by the principle of superposition of waves.
Red laser light is incident on a double slit with a slit separation of 0.35 mm.
A double-slit interference pattern is observed on a screen 2.4 m from the slits.
The distance between successive maxima on the screen is 4.7 mm.
Calculate the wavelength of the light. Give your answer to an appropriate number of significant figures.
Explain the change to the appearance of the interference pattern when the red-light laser is replaced by one that emits green light.
One of the slits is now covered.
Describe the appearance of the pattern on the screen.
The ratio = 1.5.
Show that the intensity of solar radiation at the orbit of Mars is about 600 W m–2.
Determine, in K, the mean surface temperature of Mars. Assume that Mars acts as a black body.
The atmosphere of Mars is composed mainly of carbon dioxide and has a pressure less than 1 % of that on the Earth. Outline why the greenhouse effect is not significant on Mars.
A longitudinal wave travels in a medium with speed 340 m s−1. The graph shows the variation with time t of the displacement x of a particle P in the medium. Positive displacements on the graph correspond to displacements to the right for particle P.
Another wave travels in the medium. The graph shows the variation with time t of the displacement of each wave at the position of P.
A standing sound wave is established in a tube that is closed at one end and open at the other end. The period of the wave is . The diagram represents the standing wave at and at . The wavelength of the wave is 1.20 m. Positive displacements mean displacements to the right.
Calculate the wavelength of the wave.
State the phase difference between the two waves.
Identify a time at which the displacement of P is zero.
Estimate the amplitude of the resultant wave.
Calculate the length of the tube.
A particle in the tube has its equilibrium position at the open end of the tube.
State and explain the direction of the velocity of this particle at time .
Draw on the diagram the standing wave at time .
Titan is a moon of Saturn. The Titan-Sun distance is 9.3 times greater than the Earth-Sun distance.
Show that the intensity of the solar radiation at the location of Titan is 16 W m−2
Titan has an atmosphere of nitrogen. The albedo of the atmosphere is 0.22. The surface of Titan may be assumed to be a black body. Explain why the average intensity of solar radiation absorbed by the whole surface of Titan is 3.1 W m−2
Show that the equilibrium surface temperature of Titan is about 90 K.
The orbital radius of Titan around Saturn is and the period of revolution is .
Show that where is the mass of Saturn.
The orbital radius of Titan around Saturn is 1.2 × 109 m and the orbital period is 15.9 days. Estimate the mass of Saturn.
Two microwave transmitters, X and Y, are placed 12 cm apart and are connected to the same source. A single receiver is placed 54 cm away and moves along a line AB that is parallel to the line joining X and Y.
Maxima and minima of intensity are detected at several points along AB.
(i) Explain the formation of the intensity minima.
(ii) The distance between the central maximum and the first minimum is 7.2 cm. Calculate the wavelength of the microwaves.
Radio waves are emitted by a straight conducting rod antenna (aerial). The plane of polarization of these waves is parallel to the transmitting antenna.
An identical antenna is used for reception. Suggest why the receiving antenna needs to be be parallel to the transmitting antenna.
The receiving antenna becomes misaligned by 30° to its original position.
The power of the received signal in this new position is 12 μW.
(i) Calculate the power that was received in the original position.
(ii) Calculate the minimum time between the wave leaving the transmitting antenna and its reception.